This post is the third in my DNN64 series, where I discuss my project of compiling and accelerating deep neural networks (DNNs) on the Nintendo 64 system. My first post is available here, and the goal is to use modern tools and techniques on this constrained platform. This post builds upon the challenges of limited memory discussed in the previous post, with this post looking at the memory requirements of the activation maps.

Previously we spoke about how the N64 only has 4MB of main memory by default, which creates some interesting constraints for any DNNs we want to deploy. We significantly reduced our memory requirements for the DNN parameters by modifying our code generator such that it stored the weights on disk and loaded them on demand. This means that instead of loading a full DNN model in one go, we load it partially, and free memory when it is no longer needed.

However, the weights are not the only major contributor to the memory footprint of DNNs. We also need to think about the activations. Activations are the actual input data that we pass through the DNN, which are transformed by layers and their parameters. An example of a DNN graph with activations is shown below.

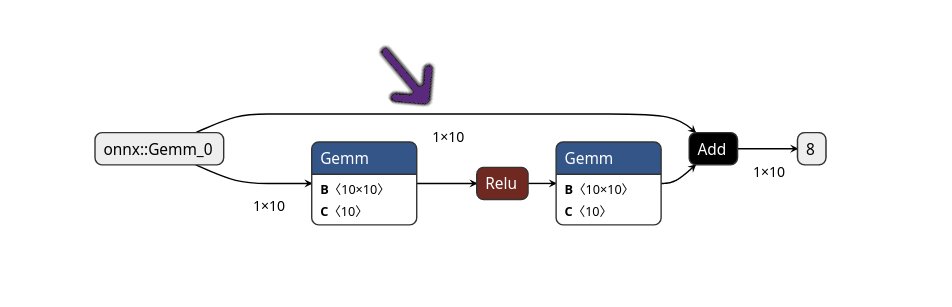
Example of a DNN.
Example of a DNN graph. Nodes are layers (and their weights), and edges are activations. Observe the purple arrow which points at a 1x10 activation matrix.

Ideally we could solve the memory requirements of our activations in a similar way to our weights: only store them for the layer they are required, and free the memory when it is no longer needed. And in principle, this is what we do. However, we have a problem: long term dependencies.

In the above graph, observe that there is a branch, where two arrows come out from the first node (onnx::Gemm_0). This means that the 1x10 activation map is used in both the first Gemm node (bottom branch), and the Add node (where the top branch and bottom branch join). Therefore we need to store that matrix for a long time, in addition to the other activations generated in the bottom branch.

For this trivial network, this isn’t really a problem, but what about for larger DNNs? Take U-Net for example, which has a “U” shape, with lots of very long term dependencies.

Sketch of the U-Net architecture.
Sketch of the U-Net architecture, with many long term dependencies.

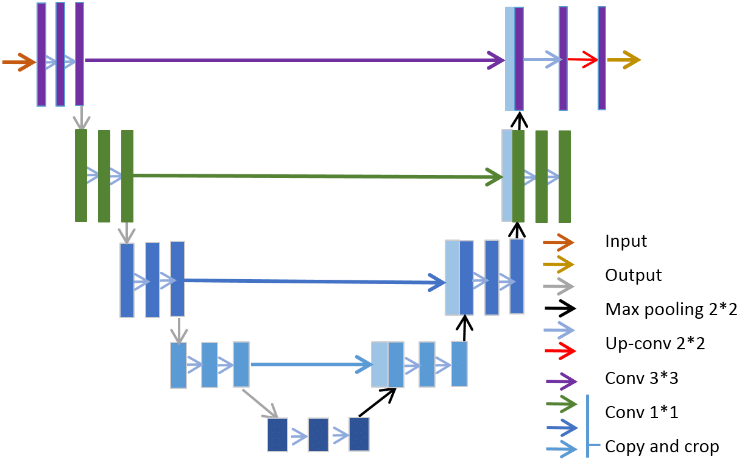
With these dependencies, it ends up being very easy to use up all of our available memory, even if the number of parameters at each layer are relatively small. If we discard the activations in-flight, then we could end up with an incorrect answer. We have to store these activations somehow until they are consumed.

We could use techniques to reduce the memory required, such as quantisation, or ephemeral sparsity. But before we think about these techniques, in this post let’s talk about memory planning.

Essentially, we need to consider what the peak amount of “scratchpad memory” we require to store the activations for our model during inference is. This will be the point where we have the largest memory footprint, potentially storing multiple activation maps. However, for many DNN architectures there are techniques we can use to reduce this peak, mostly by reordering the execution order of the computation graph.

Here’s an example of what I mean — below we have a DNN with a branch and multiple layers. I’ve labelled the intermediate activations as Small, Medium, and Large. We have the constraint that we can’t compute a given layer until all of its predecessors have been computed. But we still have choices of what order to compute the layers.

Can you see how different orderings could give different peak memory requirements?

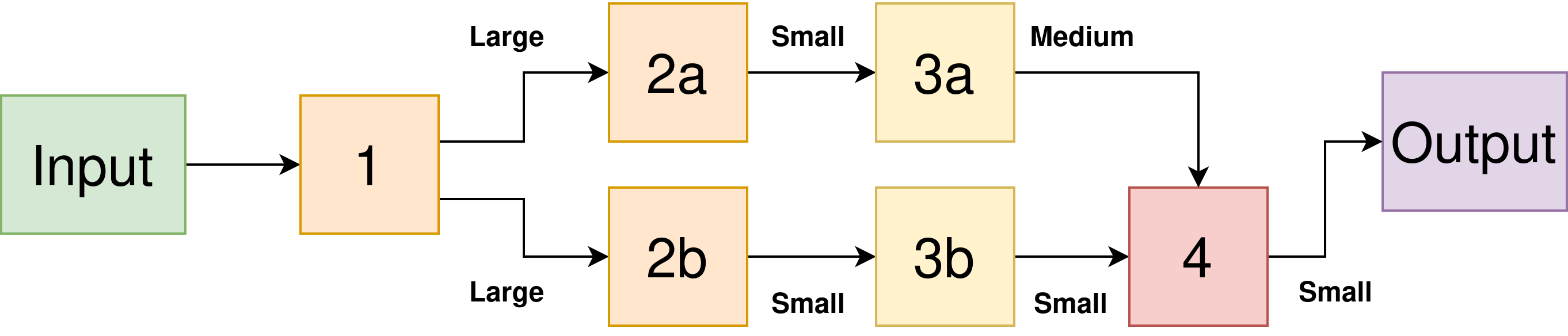
Diagram showing a branched DNN with activation maps of various sizes
Diagram showing a branched DNN with activation maps of various sizes.

If we computed the top branch first, then the second, we would compute the layers in the order:

1, 2a, 3a, 2b, 3b, and 4.

However, this has the downside that we need to store the Large activation map generated by layer 1 for a longer time, until it is consumed by our 2b computation. We also need to store the Medium activation map generated by 3a at the same time, giving us a peak activation memory requirement of Large+Medium.

Instead, a better ordering might be:

1, 2a, 2b, 3b, 3a, and 4.

This means that we can free up the Large activation map sooner, reducing our peak activation memory to Large+Small.

Hopefully that example was reasonably intuitive. However, for larger arbitrary DNNs the problem is actually quite complex, since we will have many more nodes to consider, and there may be a lot of co-optimization considerations. It is an NP-hard problem, akin to other scheduling problems such as the bin packing problem. As a result, it’s tricky to find optimal solutions. Generally the best we can do is use some heuristics.

At time of writing, Apache TVM (which we are using as the core part of our DNN compiler for the N64) has three main memory planning heuristic algorithms: greedy_by_conflicts, greedy_by_size, and hill_climb. You can see the code for them here, under src/tir/usmp/algo.

  • Greedy-by-size tries to handle the largest buffers first
  • Greedy-by-conflict tries to handle buffers which are used by multiple layers first
  • Hill climb iteratively applies greedy-by-size, trying different permutation orders to find potentially more efficient allocations.

Exploring a variety of DNNs, I found that on average the hill climb algorithm gave me the most compact memory allocation on average, but not in every case. For example, here is the required workspace for ResNet18 for ImageNet using each of the three algorithms:

Technique Workspace size (bytes)
greedy_by_conflicts 6909488
greedy_by_size 4818240
hill_climb` 4014080

Ultimately, I’ve found the peak memory of activations to be the main constraining factor for deploying on the N64. We can load our weights from the cartridge, which can be slow, but at least reduces our memory requirements (almost) as much as possible.

However, since our cartridge is read-only memory, we cannot save our input-dependent activations there. This means that our peak activations memory cannot exceed 4MB on the N64 (and probably less, since we need memory for our binary and weights).

Sure, we could save long-term activations in some sort of memory card or external storage — the N64 had an accessory called the “Controller Pak” which has 32KB of SRAM. However that is too small to really help us — our main memory is 4MB afterall, 32KB is almost a rounding error.

In conclusion, intelligent memory planning can save a lot of space for our DNN’s activations and potentially help us fit DNNs which wouldn’t fit on our platform otherwise. However, this alone won’t be enough in many cases. Given the strong memory limitation of the N64, we may require additional approaches such as quantisation and ephemeral sparsity to handle our large activation maps and fit larger models.